Monte Carlo Simulations may help you save a lot of money!

Have you ever wondered how gambling businesses always stay in business?

What is a Monte Carlo Simulation?

A Monte Carlo Method can be technically defined as a computational algorithm that rely on random sampling. Such a method can be used to solve any probabilistic interpretation. In simpler words, projecting business costs basis random variables, chances of failure for a machine, impact of launching a new product and many more could potentially be solved using the Monte Carlo method.

How do we use this?

Let’s begin with a simpler example, gambling. Whenever we talk about probability, gambling usually comes up as the first example in our head.
But, have you ever wonder why such businesses (Example - Casinos) always stay in profit? Or, why do they offer double, triple, or maybe even 10 times your invested amount as your prize money if you win the game?
Let’s take a look at it.

For this example, we’ll play a game which I’d like to call ‘Double Dice’.
The rules of this game are simple, you have to throw two dice at once, and if you get the same number on both dice, you win.
The casino decides to put a prize money of say 6 times the amount you bid on your turn if you win, and if you lose, you lose your bid amount. If you bid $10 on one roll of dice and you win, you $60, and if you lose, you lose $10. Seems like a pretty good deal, right? Well, if you look at it in terms of probability, you’ll realise that the house (Casino) always has more opportunities to win. So in this case, the total number of possible outcomes of a 2 dice roll are (6*6) = 36 and you only win in the following 6 outcomes:

1. 1,1
2. 2,2
3. 3,3
4. 4,4
5. 5,5
6. 6,6

That is, when both dice have the same number, therefore, the player can win in only 6 out of 36 outcomes.

Let’s build a Monte Carlo Simulation for this scenario.

Building a function which simulates a 3 dice roll

Now that we have simulated the main part of the game, let’s define the variables

1. SIMULATIONS = Number of times we want to simulate the entire game
2. ROLLS_PER_GAME = Number of times we want the player to roll in the entire game
3. BET_AMOUNT = The betting amount for each role
4. WIN_PROBABILITY = An array of probability of wins after each game
5. END_BALANCE = The end wallet balance of the player after each simulation
6. STARTING_BALANCE = The starting wallet balance of the player at the start of each simulation

Initiating a Plot Figure for our Simulations

Now we will begin writing our loops which will help us simulate the game. An outer for loop for running the simulation for the number of times mentioned in the ‘SIMULATIONS’ variable, and an inner while loop to keep recording the outcomes of the each dice roll within each game and adding lines to our plot figure.

Displaying the plot figure after our simulationsplt.show()

After 10,000 simulations, our figure should look similar to this:

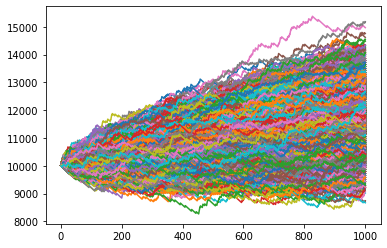
Now let’s calculate the average wallet balance for a player after 10,000 simulations:overall_win_probability = sum(WIN_PROBABILITY)/len(WIN_PROBABILITY)overall_end_balance = sum(END_BALANCE)/len(END_BALANCE)print(f"Average win probability after {SIMULATIONS} runs: {overall_win_probability}")print(f"Average ending balance after {SIMULATIONS} runs: {overall_end_balance}")

The above code would give you the following result:Average win probability after 10000 runs: 0.16678711288711615
Average ending balance after 10000 runs: 11676.773

Therefore, on an average, the player would end up earning ~$1600

Now let’s try reducing the prize money for winning, we were assuming 6 times the betting amount for the above simulation, let’s see what happens if we change 6 to 4. The new figure would look something like this:

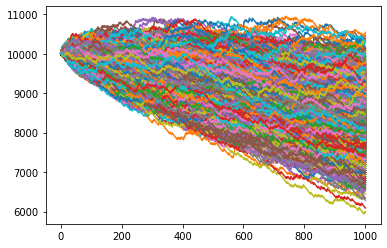
Average win probability after 10000 runs: 0.16669690309690652
Average ending balance after 10000 runs: 8333.18

Woah! What happened? We see a drastic change in the average ending balance. But, why did that happen? We can clearly see that on the basis of how much payout percentage the casino gives, we can identify what the average outcome would be by the end of night. Therefore, if the casino chooses to give 6 times / 600% of the betting amount as prize money, they would essentially lose money on an average! But, if the casino keeps the prize money at 400%, which is still pretty generous, they would end up staying at top after the night ends.

Pretty interesting, right?

---

Some other business use cases

We saw how Monte Carlo Methods can help businesses predict the outcome of events with random variables on an average thus helping them make better decisions.

Where else can we use this? There is certainly no limit to one’s imagination when it comes to applications of this method, for exampling, for a marketing manager, Monte Carlo Analysis of CAC (Cost of Acquiring a Customer) through paid marketing with variables such as Cost per lead could tell the business how much they should be paying per lead to stay profitable OR for a sales manager, after a new product is launched, this analysis with variables such as profits and expenses on selling a product in market mixed with it’s demand could help them forecast what factors need to be controlled in order to help them sell more while staying profitable.

---

Thank you for reading this article! Kindly leave a clap in case you found this interesting. :)